Section 9: LATENT DIRICHLET ALLOCATION

Pratheepa Jeganathan

04 August, 2021

theme_set(theme_minimal())
theme_update(
  text = element_text(size = 10),
  legend.text = element_text(size = 10)
)

Here, we are interested infer on the topics (bacterial communities) when we use original and modified PNA clams (two different experimental conditions). We use latent Dirichlet allocation to identify topics.

Data

In this workflow we use psE_BARBI phyloseq object in this package. In psE_BARBI, we removed DNA contaminants using BARBI.

data("psE_BARBI")
ps <- psE_BARBI

rm(psE_BARBI)

Preprocessing

We choose ASVs that have at least 25 counts in at least two specimens.

threshold <- kOverA(2, A = 25) 
ps <- phyloseq::filter_taxa(
  ps, 
  threshold, TRUE) 
## Found more than one class "phylo" in cache; using the first, from namespace 'phyloseq'
## Also defined by 'tidytree'
ps
## phyloseq-class experiment-level object
## otu_table()   OTU Table:         [ 1418 taxa and 86 samples ]
## sample_data() Sample Data:       [ 86 samples by 16 sample variables ]
## tax_table()   Taxonomy Table:    [ 1418 taxa by 6 taxonomic ranks ]
## phy_tree()    Phylogenetic Tree: [ 1418 tips and 1417 internal nodes ]
ps <- prune_taxa(taxa_sums(ps) > 0, ps)
## Found more than one class "phylo" in cache; using the first, from namespace 'phyloseq'
## Also defined by 'tidytree'
ps
## phyloseq-class experiment-level object
## otu_table()   OTU Table:         [ 1418 taxa and 86 samples ]
## sample_data() Sample Data:       [ 86 samples by 16 sample variables ]
## tax_table()   Taxonomy Table:    [ 1418 taxa by 6 taxonomic ranks ]
## phy_tree()    Phylogenetic Tree: [ 1418 tips and 1417 internal nodes ]

Edit specimen names

We edit specimen names and identify Asteraceae and non-Asteraceae plants.

sam_names <- str_replace(sample_names(ps), "E106", "E-106")
sam_names <- str_replace(sam_names, "_F_filt.fastq.gz", "")
sam_names <- str_replace(sam_names, "Connor-", "E")
sample_names(ps) <- sam_names
sample_data(ps)$X <- sam_names
sample_data(ps)$unique_names <- sam_names
aster <- c("142","143","15","ST","22","40")
non_aster <- c("33", "71", "106")

paired_aster <- c("E-142-1", "E142-1", "E-142-5", "E142-5", "E-142-10", "E142-10", "E-143-2", "E143-2", "E-143-7", "E143-7", "E-15-1", "E15-1", "ST-CAZ-4-R-O", "ST-CAZ-4-R-M", "ST-SAL-22-R-O", "ST-SAL-22-R-M", "ST-TRI-10-R-O", "ST-TRI-10-R-M")
paired_non_aster <- c("E33-7", "E-33-7", "E33-8", "E-33-8", "E33-9", "E-33-9", "E71-10", "E-71-10","E71-2","E-71-2" ,"E71-3", "E-71-3", "E106-1", "E-106-1", "E106-3", "E-106-3", "E106-4", "E-106-4")
paired_specimens <- c(paired_aster, paired_non_aster)

Choose colors for plots. We will use nine colors for nine different plants in the dataset.

plant_colors <- c("#999999", "#E69F00", "#56B4E9", "#009E73", "#F0E442", "#0072B2", "#D55E00", "#CC79A7", "purple")

Input data for LDA

Based on the ordination, we choose the number of topics as K=11. We set the hyperparameters \(\alpha = 0.8\) and \(\gamma = 0.8\).

K <- 11
alpha <- 0.8
gamma <- 0.8
stan.data <- setUpData(
  ps = ps,
  K = K,
  alpha = alpha,
  gamma = gamma
)

Posterior sampling

We need to estimate \(\theta\) and \(B = \left[\beta_{1}, \cdots, \beta_{K} \right]^{T}.\)

We estimate the parameters using HMC NUTS with four chains and 2000 iterations. Out of these 2000 iterations, 1000 iterations were used as warm-up samples.

We use high-performance computing and save the results.

We specify a file name.

fileN <- paste0(
  "JABES_Endo_all_K_",
  K,
  "_ite_",
  iter,
  ".RData"
  )
iter <- 2000
chains <- 4

stan.fit <- LDAtopicmodel(
  stan_data = stan.data, 
  iter = iter, 
  chains = chains, 
  sample_file = NULL,
  diagnostic_file = NULL,
  cores = 4,
  control = list(adapt_delta = 0.9),
  save_dso = TRUE,
  algorithm = "NUTS"
  )
save(stan.fit, file = fileN)

We extract posterior samples from the results.

samples <- rstan::extract(
  stan.fit, 
  permuted = TRUE, 
  inc_warmup = FALSE, 
  include = TRUE
  )

Alignment

We estimated the parameters using the HMC-NUTS sampler with four chains and 2000 iterations. Out of these 2000 iterations, 1000 iterations were used as warm-up samples and discarded. Label switching across chains makes it difficult to directly compute log predictive density, split-\(\hat{R}\), effective sample size for model assessment, and evaluate convergence and mixing of chains.

To address this issue, we fixed the order of topics in chain one and then found the permutation that best aligned the topics across all four chains. For each chain two to four, we identified the estimated topics pair with the highest correlation, then found the next highest pair among the remaining, and so forth.

We create a Topic \(*\) Chain matrix.

theta <- samples$theta 

aligned <- alignmentMatrix(
  theta, 
  ps, 
  K, 
  iterUse = iter/2,
  chain = chains,
  SampleID_name = "unique_names"
  )

Align topic proportion

We align the topic proportion in each specimen across four chains.

theta_aligned <- thetaAligned(
  theta, 
  K, 
  aligned, 
  iterUse = iter/2, 
  chain = chains
  )

Align ASV proportion

We align the ASVs proportion in each topic across four chains.

beta <- samples$beta 


beta_aligned <- betaAligned(
  beta, 
  K, 
  aligned, 
  iterUse = iter/2, 
  chain = chains
  )

Visualization

Plot topic proportion

Plot the topic proportion in specimens and we can save it for publication purposes. We can draw an informative summary of bacterial communities in each phenotype.

p <- plotTopicProportion(
  ps,
  theta_aligned,
  K,
  col_names_theta_all = c("iteration", "Sample", "Topic", "topic.dis"),
  chain = 4,
  iterUse = iter/2,
  SampleIDVarInphyloseq = "unique_names",
  design = ~ pna
)

ggsave(paste0("topic_dis_all_",K, ".png")), p, width = 30, height = 16)
Figure 6: Topic distribution in specimens from Sonchus Arvensis plant. The color gradient represents the median topic distribution.

Figure 6: Topic distribution in specimens from Sonchus Arvensis plant. The color gradient represents the median topic distribution.

Plot ASVs distribution

We plot the ASVs distribution in each topic.

p <- plotASVCircular(
  ps,
  K,
  iterUse = iter/2,
  chain = chains,
  beta_aligned,
  varnames = c("iterations", "topic", "rsv_ix"),
  value_name = "beta_h",
  taxonomylevel = "Class",
  thresholdASVprop = 0.008
  )

ggsave(paste0("circular_plot_plant_all_K_", K, ".png"), p, width = 28, height = 22)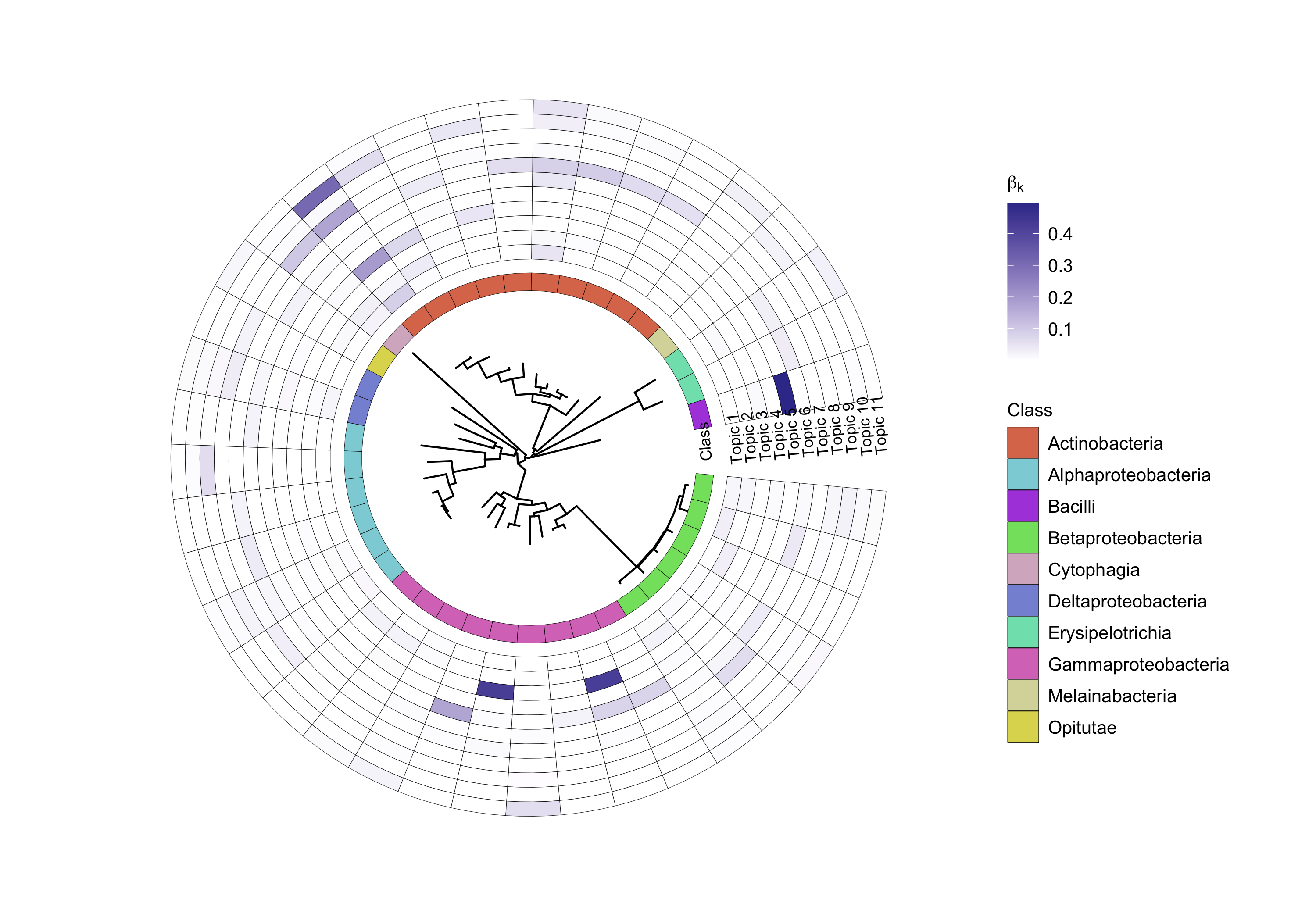
Figure 7: ASV distribution over topics in all specimens

Figure 7: ASV distribution over topics in all specimens

Model assessement

We do goodness of fit test using the posterior estimates and observed data.

p_hist <- modelAssessment(
  ps,
  stan.fit,
  iterUse = iter/2,
  statistic = "max",
  ASVsIndexToPlot = c(1, 3, 10:14, 19:26, 36, 51:53, 148)
)

ggsave(
  paste0(
    "model_assesment_hist_all_obs_sim_K_", 
    K, 
    ".png"
    ), 
  p_hist, 
  width = 12, 
  height = 6
  )
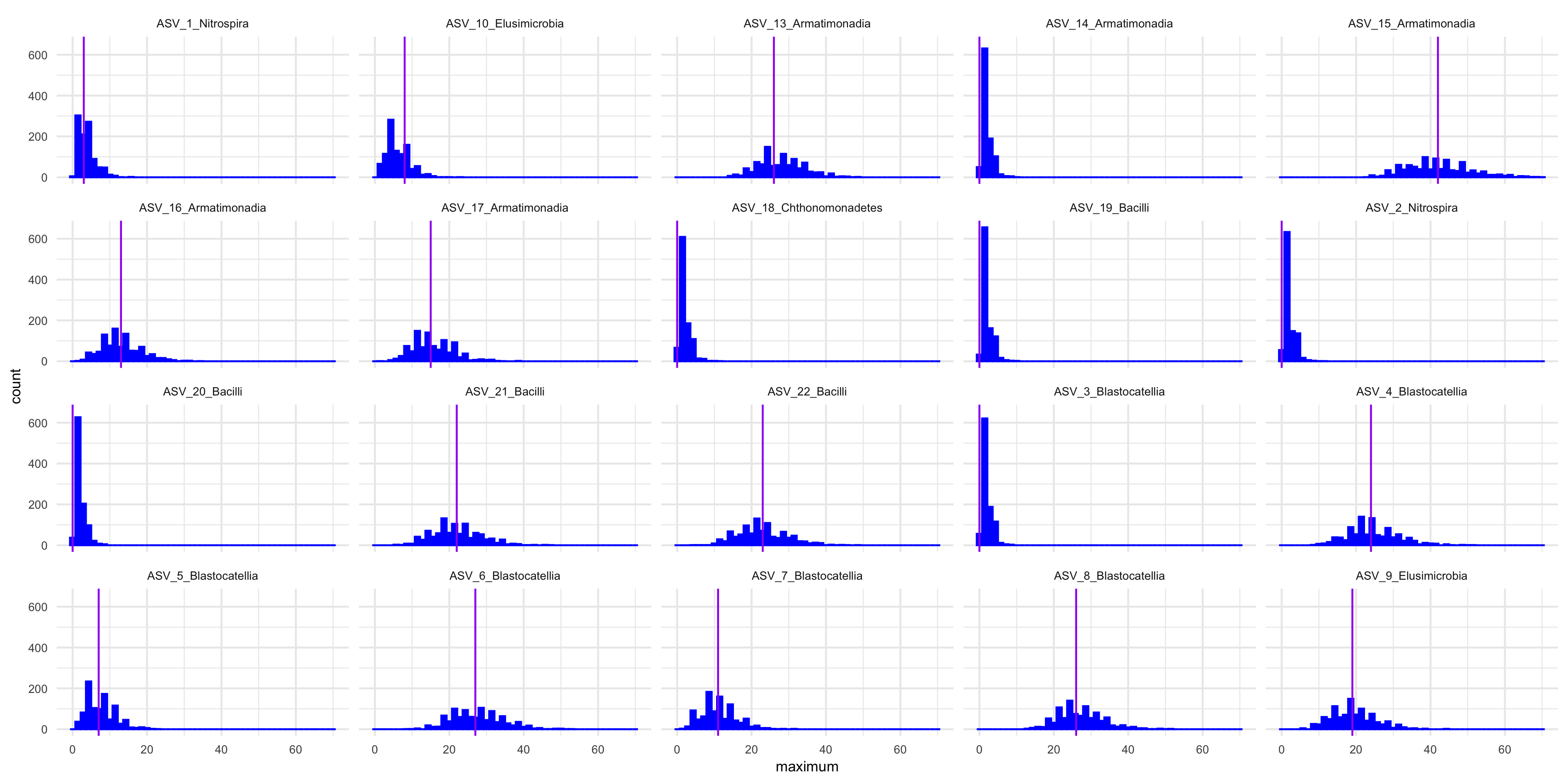
Supplementary Figure 13: Predictive model check with simulated data, observed data, and a statistic G(Kij) = max{Kij}. Each facet shows the histogram of G(Kij) of each ASV in specimens from the posterior predictive distribution and the vertical line shows the value of G (Kij ) of each ASV in observed data.

Supplementary Figure 13: Predictive model check with simulated data, observed data, and a statistic G(Kij) = max{Kij}. Each facet shows the histogram of G(Kij) of each ASV in specimens from the posterior predictive distribution and the vertical line shows the value of G (Kij ) of each ASV in observed data.

Diagnostics

Effective sample size (ESS)

We compute effective sample size for each parameter.

p <- diagnosticsPlot(
  theta_aligned = theta_aligned,
  beta_aligned = beta_aligned,
  iterUse = iter/2,
  chain = 4
)
p_ess_bulk <- p[[[1]]]

ggsave(
  paste0("ess_bulk_plant_all_K_", K, ".png"), 
  p_ess_bulk, 
  width = 9, 
  height = 6
  )
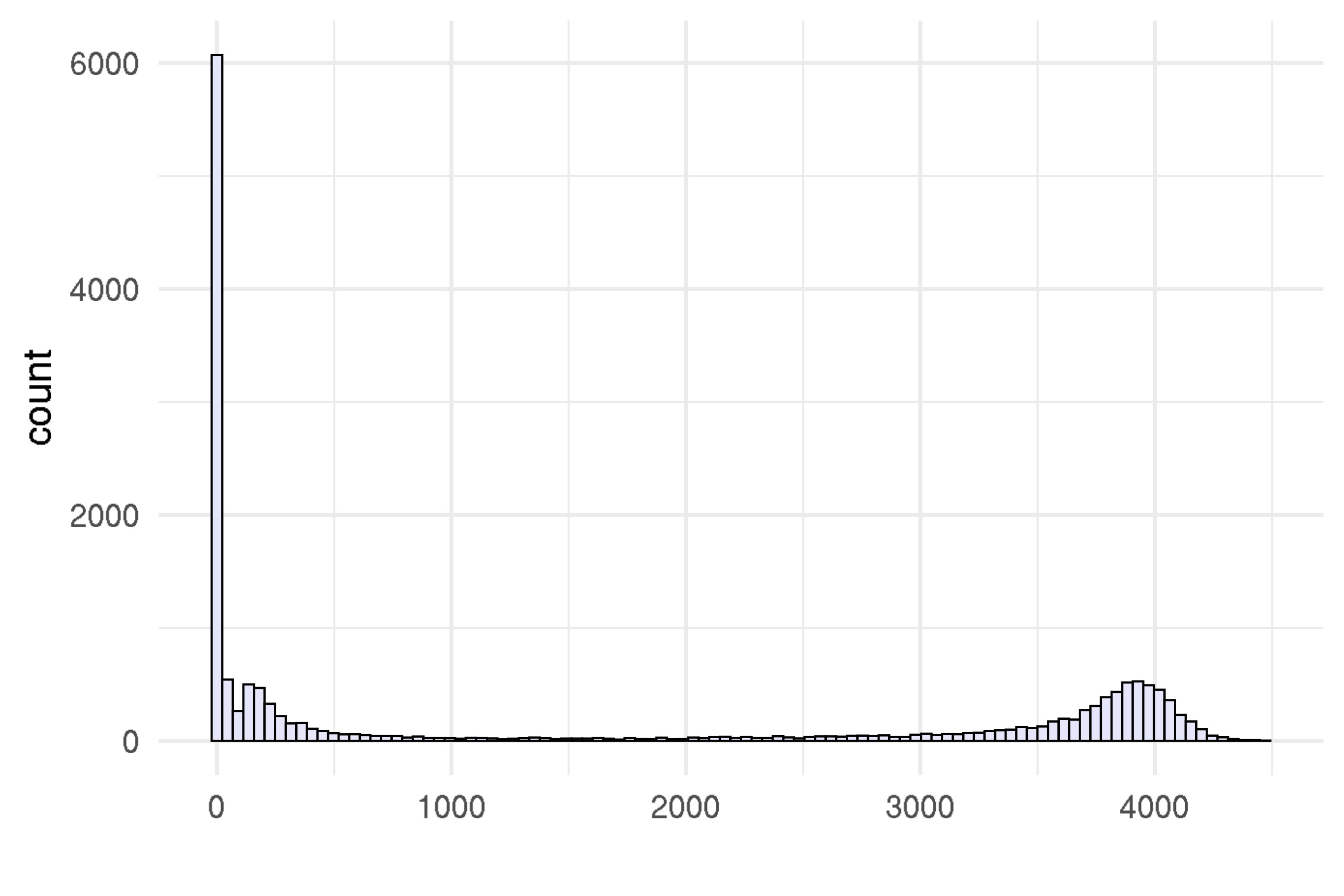
Supplementary Figure 14: Effective sample size (ESS) with eleven topics.

Supplementary Figure 14: Effective sample size (ESS) with eleven topics.

\(\hat{R}\)

We can check whether \(\hat{R}\) is less than 1.02.

p_rhat <- p[[2]]

ggsave(
  paste0("Rhat_plant_all_K_", K, ".png"), 
  p_rhat, 
  width = 9, 
  height = 6
  )
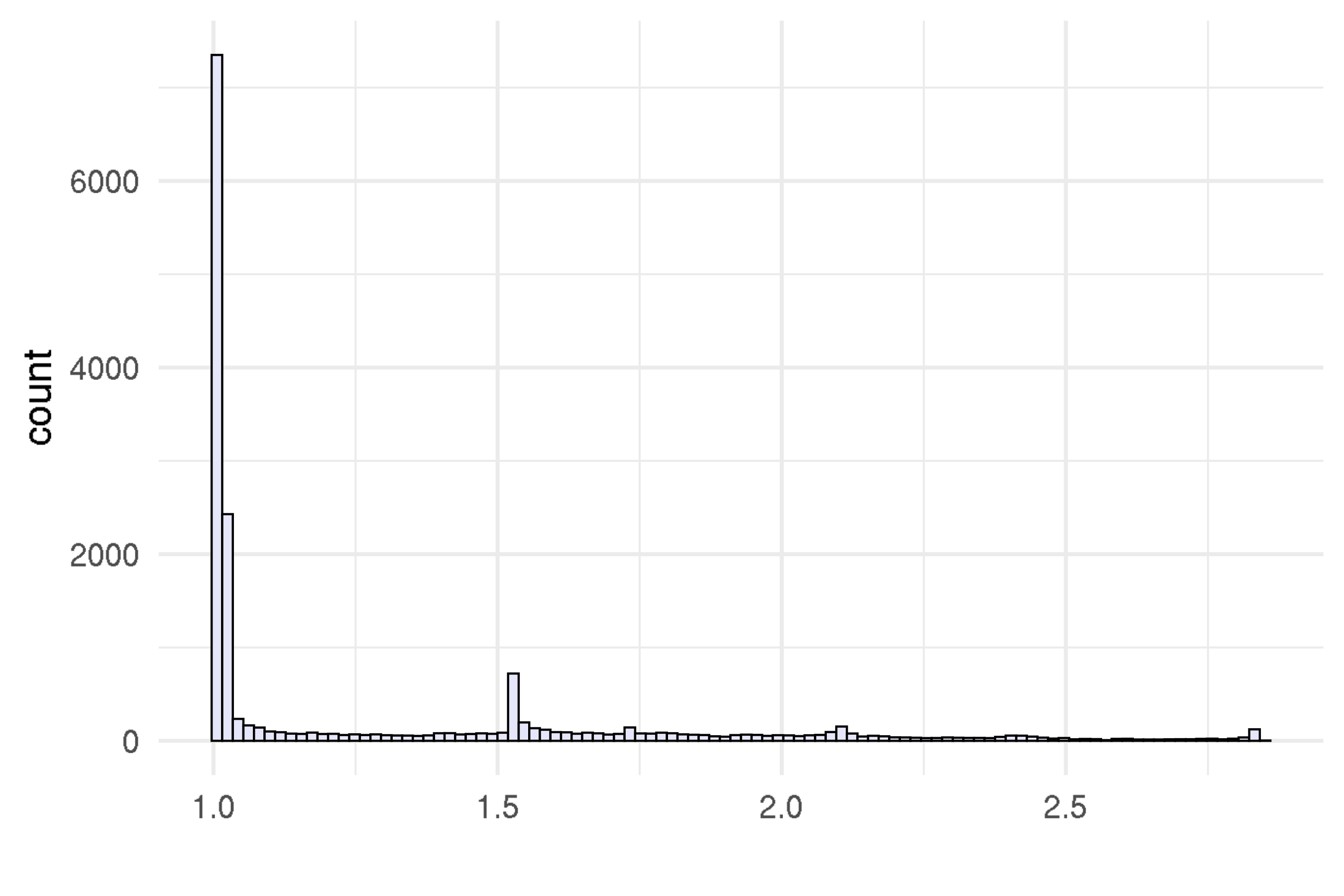
Supplementary Figure 15: Split Rhat with eleven topics.

Supplementary Figure 15: Split Rhat with eleven topics.

Differential topic analysis

Test on all specimens

We do test on all specimens. We can write DESeq2 results to LaTex.

dds_all <- diffTopAnalysis(
  design = ~ pna,
  ps,
  theta_aligned,
  subsetSample = sample_names(ps),
  fitType = "mean"
)

saveRDS(
  dds_all, 
  file = paste0("dds_all_K_", K,".rds")
  )
data("dds_all_K_11")
res <- results(dds_all_K_11)
res 
## log2 fold change (MLE): pna O vs M 
## Wald test p-value: pna O vs M 
## DataFrame with 11 rows and 6 columns
##            baseMean log2FoldChange     lfcSE      stat      pvalue        padj
##           <numeric>      <numeric> <numeric> <numeric>   <numeric>   <numeric>
## Topic_1  12980.2689      -0.902957  0.954118 -0.946379 3.43955e-01 0.609485512
## Topic_2   1388.4912       0.328641  0.691155  0.475495 6.34434e-01 0.719579869
## Topic_3     14.5487      -0.559488  0.584374 -0.957414 3.38358e-01 0.609485512
## Topic_4   6138.5557       2.056851  0.749974  2.742564 6.09615e-03 0.022352555
## Topic_5     50.1848       2.693638  0.665150  4.049672 5.12894e-05 0.000564184
## Topic_6   5002.9019      -0.285674  0.795705 -0.359020 7.19580e-01 0.719579869
## Topic_7     25.1418      -0.382548  0.498956 -0.766696 4.43262e-01 0.609485512
## Topic_8    642.9452       0.638403  0.749673  0.851575 3.94450e-01 0.609485512
## Topic_9    728.3070       0.780513  0.781941  0.998174 3.18195e-01 0.609485512
## Topic_10  2452.9197       2.617431  0.725300  3.608757 3.07668e-04 0.001692175
## Topic_11  6788.9347       0.330308  0.782177  0.422294 6.72811e-01 0.719579869
#writeResTable(res, fileN = paste0("dds_all_K_", K,".tex"))

Test on paired-specimens

We do the test on paired-specimens.

dds_all_paired <- diffTopAnalysis(
  design = ~ pna,
  ps,
  theta_aligned,
  subsetSample = paired_specimens
)
 
saveRDS(
  dds_all_paired, 
  file = paste0("dds_all_paired_K_", K,".rds")
  )
data("dds_all_paired_K_11")
res <- results(dds_all_paired_K_11)
res 
## log2 fold change (MLE): pna O vs M 
## Wald test p-value: pna O vs M 
## DataFrame with 11 rows and 6 columns
##           baseMean log2FoldChange     lfcSE      stat      pvalue        padj
##          <numeric>      <numeric> <numeric> <numeric>   <numeric>   <numeric>
## Topic_1  3983.7697      -9.412600  1.056278 -8.911103 5.05275e-19 5.55802e-18
## Topic_2   898.6700       1.491941  0.999725  1.492352 1.35607e-01 2.13097e-01
## Topic_3    23.5763       0.282751  0.924598  0.305810 7.59749e-01 8.12226e-01
## Topic_4  1138.7952       3.371133  0.995722  3.385618 7.10182e-04 1.95300e-03
## Topic_5    31.7514       2.290040  0.892339  2.566333 1.02780e-02 1.88430e-02
## Topic_6    83.5973       0.351490  0.912658  0.385128 7.00143e-01 8.12226e-01
## Topic_7    35.3625       0.233201  0.801434  0.290979 7.71067e-01 8.12226e-01
## Topic_8   393.8606      -0.265216  1.116438 -0.237556 8.12226e-01 8.12226e-01
## Topic_9   468.2304      -6.004885  0.944671 -6.356589 2.06282e-10 7.56369e-10
## Topic_10 1938.0794       3.029427  1.085621  2.790502 5.26263e-03 1.15778e-02
## Topic_11  419.7516       6.324962  0.940052  6.728314 1.71641e-11 9.44024e-11
#writeResTable(res, fileN = paste0("dds_all_paired_K_", K,".tex"))

Test on paired non-Aster specimens

We do the test on paired non-Aster specimens.

dds_all_paired_nonaster <- diffTopAnalysis(
  design = ~ pna,
  ps,
  theta_aligned,
  subsetSample = paired_non_aster
)


saveRDS(dds_all_paired_nonaster, 
        file = paste0("dds_all_paired_nonaster_K_", K,".rds")
        )
data("dds_all_paired_nonaster_K_11")
res <- results(dds_all_paired_nonaster_K_11)
res 
## log2 fold change (MLE): pna O vs M 
## Wald test p-value: pna O vs M 
## DataFrame with 11 rows and 6 columns
##            baseMean log2FoldChange     lfcSE        stat      pvalue       padj
##           <numeric>      <numeric> <numeric>   <numeric>   <numeric>  <numeric>
## Topic_1   860.20984    -0.00301489  1.571767 -0.00191815 0.998469536 0.99846954
## Topic_2  1040.00766    -0.23883154  1.489550 -0.16033804 0.872614794 0.99846954
## Topic_3     4.72578    -1.96488007  1.042164 -1.88538517 0.059377854 0.16328910
## Topic_4   180.11478     4.32606625  1.204541  3.59146455 0.000328825 0.00361707
## Topic_5    27.56455     2.23657681  1.180879  1.89399299 0.058225941 0.16328910
## Topic_6     6.67586     0.09843585  0.881377  0.11168412 0.911073873 0.99846954
## Topic_7     5.19734    -0.59432231  0.892778 -0.66569966 0.505603089 0.79451914
## Topic_8   425.39352     0.63277929  1.509760  0.41912576 0.675124224 0.92829581
## Topic_9  2991.31585    -2.69366584  1.665720 -1.61711797 0.105852819 0.19406350
## Topic_10 1417.10667     2.41994794  1.495368  1.61829572 0.105598883 0.19406350
## Topic_11   33.61182     3.26394880  1.158670  2.81697937 0.004847764 0.02666270
#writeResTable(res, fileN = paste0("dds_all_paired_nonaster_", K,".tex"))

Test on paired Aster specimens

We do the test on paired Aster specimens.

dds_all_paired_aster <- diffTopAnalysis(
  design = ~ pna,
  ps,
  theta_aligned,
  subsetSample = paired_aster
)


saveRDS(
  dds_all_paired_aster, 
  file = paste0("dds_all_paired_aster_K_", K,".rds")
  )
data("dds_all_paired_aster_K_11")
res <- results(dds_all_paired_aster_K_11)
res 
## log2 fold change (MLE): pna O vs M 
## Wald test p-value: pna O vs M 
## DataFrame with 11 rows and 6 columns
##           baseMean log2FoldChange     lfcSE       stat      pvalue        padj
##          <numeric>      <numeric> <numeric>  <numeric>   <numeric>   <numeric>
## Topic_1  6218.5368    -10.4304467   1.51290 -6.8943421 5.41147e-12 5.95261e-11
## Topic_2   808.8041      1.2913524   1.35518  0.9529025 3.40639e-01 6.24506e-01
## Topic_3    62.3447      0.5769415   1.41106  0.4088702 6.82635e-01 8.34332e-01
## Topic_4  3197.9976      0.9723636   1.53691  0.6326749 5.26946e-01 8.28058e-01
## Topic_5    10.5337     -0.1502755   1.27513 -0.1178511 9.06186e-01 9.48164e-01
## Topic_6   188.5282      0.0862107   1.32605  0.0650131 9.48164e-01 9.48164e-01
## Topic_7    20.2758      0.4522516   1.03245  0.4380355 6.61361e-01 8.34332e-01
## Topic_8    12.0123     -1.3189221   1.02924 -1.2814486 2.00036e-01 4.52427e-01
## Topic_9  1035.0590     -7.8134758   1.32604 -5.8923438 3.80756e-09 1.39610e-08
## Topic_10  129.1210     -1.5272929   1.20675 -1.2656214 2.05649e-01 4.52427e-01
## Topic_11 2344.2823      8.3837719   1.38843  6.0383030 1.55743e-09 8.56589e-09
#writeResTable(res, fileN = paste0("dds_all_paired_aster_", K,".tex"))