Multivariate Saddlepoint Density Approximation (MSAP)
The AR models are typically used to model the time series data. Several possible procedures exist for estimating model parameters. We refer to some of them as Yule-Walker (YW) estimators (Yule, 1927), least squares estimators, Burg estimators (Burg, 1968), and maximum likelihood estimators. Although the YW estimators produce bias in the estimation, this is a commonly used estimation method in practice.
Application
Once the AR model is fit to the data, it is common to check the significance of model parameters. We then identify the order of the AR model.
Method
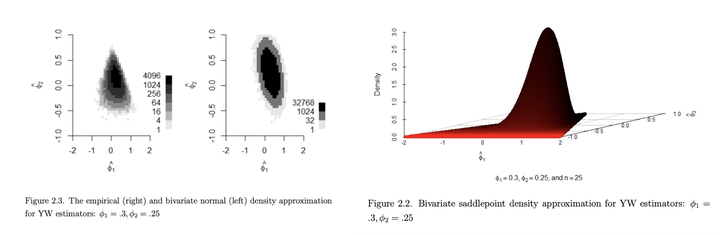
We derive the bivariate saddlepoint density approximation for the YW estimators of AR(2) model parameters. First, we write the sample autocorrelation as the ratio of quadratic forms. Then, we substitute this ratio in the YW equations and derive a system of quadratic estimating equations (QEE). Next, we show that the YW estimators of AR(2) model parameters are roots of QEE. We also show that the Jacobian of the transformation of the QEE coordinate space to the parameter coordinate space is positive semi-definite. Finally, we derive the bivariate saddlepoint density approximation using that of QEE.
Software
- PhD dissertation Chapter II supplement.
Paper
- PhD dissertation Chapter II.